PRÁCTICA 6: CIRCUITOS DE 2º ORDEN

1. Introducción

En esta práctica vamos a ver cómo se comportan las dos configuraciones (serie y paralelo) de los circuitos RLC de segundo orden.

Las ecuaciones que utilizaremos para hallar los valores que se nos pidan serán estas dos, dependiendo de si estamos trabajando en un circuito RLC en serie o en paralelo:

Serie: 

(Siendo “ζ” el coeficiente de amortiguación)

2. Ejercicios.

2.1. Respuesta de un circuito RLC serie.

Caso A: Sistema sobreamortiguado

Debemos simular el siguiente circuito realizando un análisis tipo Time Domain (Transient) durante 10ms o más y nos pide que mostremos en la gráfica la corriente que pasa a través de la resistencia R1 para comprobar que se trata de una respuesta sobreamortiguada. Además debemos calcular el valor de ζ en este caso.

Para cambiar los valores de IC (Initial Condicion o condición inicial) debemos hace doble click sobre es componente que deseemos editar y aparece la siguiente pantalla:

A la derecha, bajo IC debemos colocar el valor deseado (si queremos que se muestre en la pantalla de diseño debemos darle a click derecho sobre el cuadro, clickar en display y decirle que muestre el valor, y nombre y a continuación darle a aceptar).

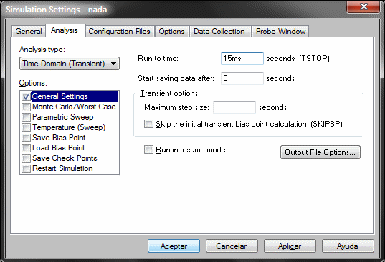
Colocamos un amperímetro antes de la resistencia y configuramos la simulación pulsando en el desplegable de la barra llamado Pspice:

Por último lanzamos la simulación pulsando el botón de play

Claramente la gráfica representa claramente una respuesta sobreamortiguada de un circuito RLC, y para el cálculo del valor de “ζ” simplemente sustituimos los datos en la ecuación respectiva:

Como el valor de “ζ” es mayor de 1 el circuito es sobreamortiguado.

 

Caso B: Sistema subamortiguado

Para este caso nos debemos modificar prácticamente las condiciones de simulación, solo hay que cambiar el valor de la resistencia R1 a 1Ω.

Si lanzamos la simulación  nos muestra la siguiente gráfica:

Como vemos es la clásica respuesta subamortiguada, y si hallamos el valor teórico de ζ:

También comprobamos que es un valor menor que 1, lo que coincide con lo que nos muestra la gráfica.

Caso C: Sistema críticamente amortiguado

Aquí nos piden que calculemos el valor de R1 para que el circuito sea críticamente amortiguado, o sea, para que ζ sea igual a 1.

Si aplicamos la formula de los anteriores apartados nos da que R1 ha de ser igual a 10, así que le damos ese valor a la resistencia y lo simulamos:

 Con su gráfica respectiva:

2.2. Respuesta de un circuito RLC paralelo

Caso A: Sistema sobreamortiguado

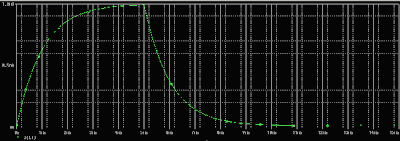
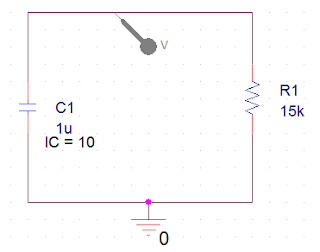
Ahora debemos diseñar el siguiente circuito y realizar una simulación Time Domain (Transient) durante 150 ms o más (en algún caso será necesario para ver la gráfica con mayor claridad) para visualizar la tensión en los extremos del condensador.

Ahora colocamos el indicador de voltaje en el nodo superior y realizamos la simulación (en este caso durante 200ms).

Si aplicamos la formula para el RLC en paralelo veremos que ζ es mayor que 1 y que por tanto es sobreamortiguado.

Caso B: Sistema subamortiguado

En este punto se nos pide que calculemos el valor que ha de tener R1 para que ζ sea menor que 1, y más en concreto, el valor que toma R1 cuando ζ es igual a 0.6, por tanto sustituimos ζ en la ecuación para paralelo y nos da como resultado 4166.66... periodico, pero redondeamos a dos decimales, 4166,67.

A continuación hay que realizar la simulación y ver que gráfica resulta. Cambiamos el valor de R1 por 4166,67 y lanzamos la simulación.

Como se puede ver en respuesta subamortiguada el valor de Vc decrece con mayor velocidad que en el caso subamortiguado.

Caso C: Sistema críticamente amortiguado

Este caso es similar al anterior solo que debemos calcular el valor de R1 cuando ζ vale 1 (lo cual quiere decir que la respuesta del sistema es críticamente amortiguada) y que lo simulemos.
Volvemos a sustituir en la ecuación, la cual nos indica que R1 debe ser 2500 si ζ es igual a 1.
Le damos el valor obtenido a R1 y realizamos la simulación.

Con esto podemos comprobar que la celeridad con la que Vc desciende se encuentra en un punto medio entre la respuesta sobreamortiguada y la subamortiguada.

PRÁCTICA 5 (ejercicios 4-5): CIRCUITOS DE PRIMER ORDEN

4. Circuito de carga y descarga de un condensador

   4.1 Circuito de carga y descarga de un condensador con interruptores

  

Debemos de crear un circuito como el que veremos a continuación en el cual hemos utilizado los mismos componentes que en la actividad 3.1 y 3.2, añadiéndole dos interruptores que se encuentran en la librería EVAL con el nombre de Sw_tOpen y Sw_tClose y cambiar los valores de todos nuestros componentes a los de la siguiente imagen.(El condensador debe tener IC=0V).

Los dos interruptores conmutaran a t = 5ms por lo que vamos a apreciar la curva de carga y descarga que realiza este circuito hasta t = 15ms, para ello tenemos que colocar un medidor de voltaje en el comienzo borne positivo del condensador.

Una vez colocado el medidor podemos comenzar a configurar el análisis, para ello abriremos crearemos un nuevo proyecto de simulación.

Se abrirá una nueva ventana en la que deberemos poner el nombre del proyecto y posteriormente configuraremos el análisis de tipo “Time Domain” y modificaremos el tiempo de análisis(Run to time) a 15ms.

Una vez hecho esto haremos click en el botón “Play”

Comenzará a realizarse el análisis y nos aparecerá una nueva ventana con la siguiente gráfica en la que podemos ver la carga y la descarga del condensador.

   4.2 Circuito de carga y descarga de un condensador mediante generador de tensión

Esta actividad consiste en analizar la carga y descarga de un condensador en un circuito sin interruptores y cambiando la fuente de tensión VDC por un generador por pulsos de tensión VPULSE. El circuito debe de ser como el de la siguiente imagen.

Tras haber creado nuestro circuito queremos analizar la carga y descarga del condensador y también analizar los pulsos de el generador de tensión, para ello debemos colocar dos medidores de voltaje: uno en el condensador y otro en el generador de corriente.

Una vez colocados los medidores crearemos un nuevo proyecto de simulación, como en el ejercicio no nos lo especifica pondremos como tiempo de duración 5ms en modo Time Domain y nos aparecerá la siguiente gráfica siendo la gráfica de color verde la carga y descarga del condensador y la gráfica roja los pulsos del generador de tensión.

   5. Carga y descarga de una bobina.

Para realizar este ejercicio nos dice que tenemos que utilizar el circuito de la actividad 4.1 cambiando el condensador por una bobina, de modo que, el valor de la constante del tiempo sea igual con la bobina que con el condensador, por ello, tendremos que cambiar el valor de la bobina a 10H.

Una vez construido el circuito, el ejercicio nos pide visualizar la curva de carga y descarga en el, por lo que deberemos colocar un medidor de intensidad en el inicio de la bobina.

Una vez hecho esto, debemos crear un nuevo perfil de simulación de tipo Time Domain, con el mismo tiempo de análisis que en la actividad 4.1 (t = 15 ms).

Cuando hayamos configurado la simulación, se iniciara el análisis con el botón

, y nos aparecerá la siguiente gráfica:

PRÁCTICA 5 (ejercicios 1-3): CIRCUITOS DE PRIMER ORDEN

Creamos una carpeta para la practica 5.

-Luego cogemos y abrimos el orcad capture

-A continuación vamos a File, New, Proyect.

-En Name ponemos el nombre que queremos para el archivo en este caso Practica 5.

-Y seleccionamos la opción de Analog or mixed A/D
-Y donde dice location C:\Users\FranciscoJose\Desktop\practica pspice 5 y 6

 En la siguiente ventana le damos a créate a blank Project y le damos a ok.

2. Carga de un condensador

Ahora vamos a la librería source y escribimos VDC que seria nuestra alimentación

Luego escribimos analog y en ella se encuentra con la R la resistencia y con la C el condensador

 Después damos doble click a la R y colocamos el valor 15k

 Y al condensador una 1u

Para indicar que el condensador parte de carga 0v, damos doble click en la imagen del condensador y colocamos en IC a valor 0V

2.1. Carga de C

Vamos a Pspice y New simulation profile creamos el nombre del archivo y a continuación seleccionamos time Domain y  modificamos el tiempo de simulación a 100milisegundos.

Ahora vamos al icono y lo colocamos en el circuito justo delante del condensador.

Le damos al botón simular y nos saldrá la gráfica siguiente y el circuito con los valores de tensión en los diferentes nodos.

 En la grafica se puede observar como el condensador se carga.

2.2 Carga de C

Cambiamos los valores de la resistencia a 1.5k, el condensador a 5u y la fuente a -3Vdc

Cambiamos y nos da esta gráfica.

 2.3 Estudio de la constante de tiempo de carga.

Realizamos un análisis paramétrico del primer circuito.

Buscamos en la parte de librerías la palabra PARAM y nos aparecerá un icono que debemos colocar en el circuito y cuando lo tenemos le damos doble click sobre el y nos llevara a una pantalla donde podemos elegir nuevas variables para que el propio programa calcule el valor necesario de esa variable para ese circuito.

 Vamos a la variable creada y con el botón derecho sobre ella le damos a display y nombre y valor .

 Vamos a simular el circuito y para ello vamos a new simulation y seleccionamos parametric sweep donde le damos a global parameter y le damos el nombre de la variable, el tipo de progresión que es lineal y después el intervalo de valores de 1k hasta 20k omh con incremento de 1k.

Simulamos el circuito y nos da la siguiente gráfica del condensador

 Al ir incrementando la resistencia tarda más en cargar por lo que la curva de carga es menos pronunciada.

3 Descarga de un condensador.

Montamos el circuito con un condensador de 1u y un voltaje de 10v iniciales y colocamos una resistencia de 15k omh.

Para colocar la IC lo hacemos como siempre doble click sobre el condensador y en IC colocamos 10.

Como se puede observar el condensador se va descargando progresivamente hasta obtener el valor 0V.